Calculate slope gradient and curvature, and hills

Source: R/flow_05_slope_gc.R

Computes row (east/west) and column (north/south) slope gradients and curvatures. Also calculates hill slopes as points when slope gradients switch directions

slope_gc(db, grid = 1)

Arguments

db

Dataframe dem
grid

Numeric. Grid size for the original dem

Details

Assume the following cells, and the calculations on elevation for focal point 5:

c7 c8 c9

c4 c5 c6

c1 c2 c3

Slope gradients and curvature

  • Row slope gradient towards east (sgre): (c4 - c6) / (2 * grid)

    • Positive slope is downslope (and east-facing)

    • Negative slope is upslope (and west-facing)

  • Row slope gradient (sgr): abs(sgre)

  • Column slope gradient towards north (sgcn): (c2 - c8) / (2 * grid)

    • Positive slope is downslope (and north-facing)

    • Negative slope is upslope (and south-facing)

  • Column slope gradient (sgc): abs(sgcn)

  • Row slope curvature (scr): (2 * c5 - c4 - c6) / (grid^2)

  • Column slope curvature (scc): (2 * c5 - c2 - c8) / (grid^2)

Where missing neighbours, assume same elevation as central point (i.e. assume an extension of the field).

Zero values replaced with arbitrarily small value, 0.00001

For gradients, zero values replaced with arbitrarily small value (0.00001) but with the sign of the previous point (i.e. to left (n4, west) if row; to bottom (n2, south) if column). If that previous point is missing, look to next point (i.e. n6 or n8). If cannot resolve by working through points, assign to positive.

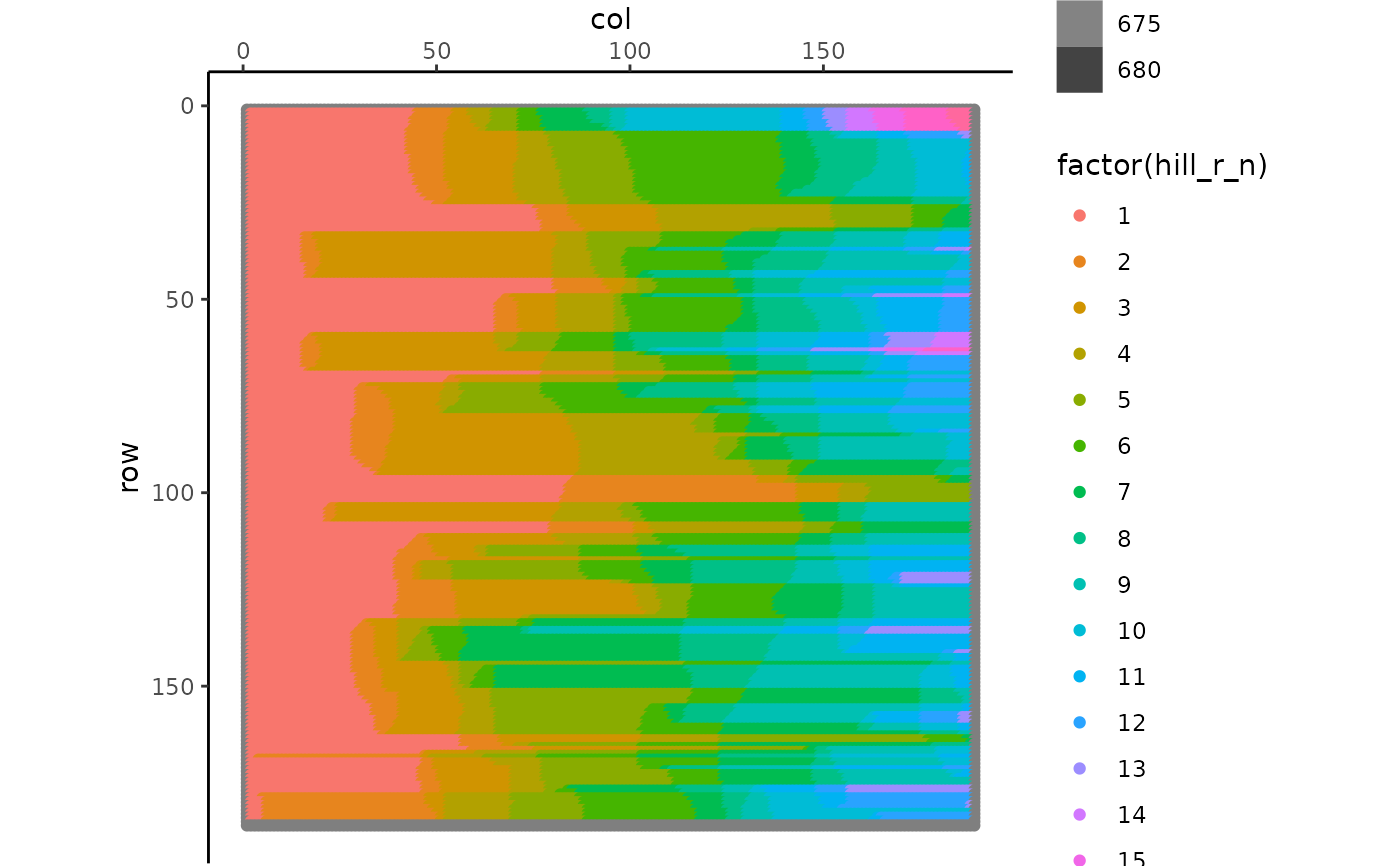
Hill slopes

  • hill_r_n: Number of hillslopes in that row. It goes from 1 to whatever it ends. Hillslope number changes when it goes from downslope to upslope or from upslope to downslope (SGRE changes sign)

  • hill_r_dir: Direction the slope is facing, east facing as 2 and west facing as 4, all cells with the same hillslope no. have same hillslope direction

  • hill_r_cell: Order number of the cell in the hillslope, starts from 1 to how many cells there are in a given hillslope

  • hill_c_n: Same as for row, changes when SGCN changes sign

  • hill_c_dir: Same as for row, north facing as 1 and south facing as 3

  • hill_c_cell: Same as for row.

Directions:

N (1) -> E (2) -> S (3) -> W (4)

Examples


d <- slope_gc(test_dem)

library(ggplot2)
flow_plot(d, type = "elevation") +
  geom_point(aes(colour = factor(hill_r_n)))